Copied Source Check and Untranslatable Text Check options
Copied Source and Untranslatable Text Check options are part of the Transcheck feature in Wordfast Pro. They can be set in Transcheck preferences control pane at the project level. The Copied Source option serves to identify segments in the target that contains segments copied from the source. Untranslatable Text Check verifies the consistency of the untranslatable content in the source and target segments.
Configuring Copied Source Check
To customize the copied source checking operation from the Preferences option:
- Click on
 to open Preferences.
to open Preferences. - In the Preferences dialog, click Transcheck under “New Project Preferences”.
- Scroll down and select Copied Source Check.
The related options appear as shown:
Select any options that apply from the following list:
- Skip exact matches — Select to ignore exact matches of copied source content.
- Skip context matches — Select to ignore context matches of copied source content.
- Skip tokens — Select to ignore software tokens within regular expressions in the copied source, such as [-+_/\[\]()#:;.A-Z0-9]+
Note: Skip tokens is used as an exception to Copied Source Check when an entire segment consists of text that is code-like and shouldn’t be translated. The given regex for this option, [-+_/\[\]()#:;.A-Z0-9]+, prevents segments that contain only numbers, all uppercase letters, certain punctuation, and mixtures of all of these categories from being marked as untranslated copied source segments. A specific example would be a segment containing just a product part number such as BD01-003145 that gets copied straight to the target.
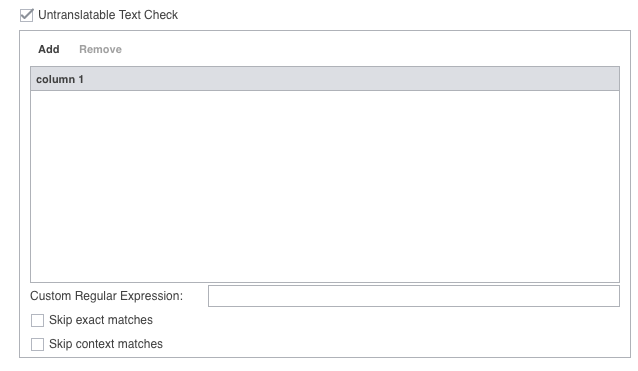
Untranslatable Text Check
To configure the handling of untranslatable text checking from the Preferences option:
- Click on
 to open Preferences.
to open Preferences. - In the Preferences dialog, click Transcheck under “New Project Preferences”.
- Scroll down and select Untranslatable Text Check.
The Untranslatable Text Check option expands to a dialog box.
- To retain the untranslatable text in the target segment, click Add.
- Enter the untranslatable text to be retained.
- Enter a custom regular expression as necessary.
- To remove untranslatable text from the check, highlight the text in the list and click Remove.
- Select any of the following options that apply:
- Skip exact matches — Select to ignore exact matches of untranslatable regular expressions.
- Skip context matches — Select to ignore context matches of untranslatable regular expressions.
The Untranslatable Text Check is used to list individual items that within any segment should remain untranslated or unmodified in the target. Examples would be a company name, a product name, a source term that gets used as a loan word in the target, or a variable (e.g., $name) in a code string. Skip exact matches and Skip context matches are exceptions to the rule so that exact and context match target segments are not checked (because these are usually already translated and verified segments).
Custom Regular Expression: As opposed to making a long list of individual items, a regex can be used to specify a category of items. With the $name example from above, all untranslatable variables of that type (e.g., $number, $date, etc.) could be identified with a regex, such as \$[a-z]+.